
新年あけましておめでとうございます。
2021年は良き1年にしたいと、CUBEの変なの担当の杉本です。
年末年始の過ごし方
年末年始、皆様はいかがお過ごしでしたか?
私、杉本は座り込んで考え事と、2020年の流行り技術で見ていなかった分野のキャッチアップや、久々のフライトシムでグアムから羽田、羽田から熊本と飛び回っておりました。
ため込んでいた動画やアーカイブの処理もできたのでオタ….Geek的には満足できるお休みでした。
今回はそんな「座り込んで考え事」の中で、なぜか疑問に思ったことを追求してみようと思います。
それは、「穴」は裏返す事が可能であるのか、仮に裏返すことに成功したとしてそれを証明できるのか考えてみます。
※なお、筆者は数学や物理学は好きですが、別に詳しいわけでもないので、真に答えを探りたい方は数学の先生方をあたってください。
まずは穴を定義してみる。
「穴」とは、どこにだってあるが、その形態も様々であるのでモデルケースとして、穴の定義を試みた。
今回は単純に次の様に定義する。
・3次元の直行座標空間において存在する物体の断面を観測した際に、その物体に周囲を完全に囲まれた非物理的実体である空間
めんどくさいので一言で「鉄パイプ」(以下、パイプ)と定義する。
パイプの断面には、一般的解釈では穴が存在する。
素直に裏返しを試みる。
ここに、パイプを自由に伸縮出来る人がいたとする。
パイプを洋服の袖を折り返す様に変形させ、内側の穴に面したいた面をかつての表面に反転できたとする。
この場合に、「穴」の裏返しに成功したといえるだろうか。
残念ながらこれは、「穴」を裏返したとは言えないのではないだろうか?
少なくとも私は「穴」を裏返した事を証明する方法を思いつかない。
数学的な操作として、面を裏返したことは表現できるが、穴は確かにそこに存在する。
仮に穴を反転したとすれば、穴を観測していた者からは穴が消失するのではないだろうか。
誰であっても、落とし穴を見たら「穴」だと思うが、それに落ちてからは外の世界を「穴」とは認識しないはずだ。
よってこの素直な試みは、論理的に失敗したのではないだろうか?
穴を無限大に拡大してみる。
正直に言うと、素直な裏返しの試みの時点で無理な感じがしてくる。
「穴」を無限大に拡大してみるとどうだろうか?
が、これはダメだ。
穴を拡大しても観測者が不変である以上は、絶対に穴を認識することが出来る。
だが、これはなんかイケル気がする。
逆に無限小に縮小してみる。
逆のことをしてみるとどうだろう?
無限小の穴が存在するとするとどうだろうか。
これも同様に観測者が不変であるならば、穴は観測可能なのでやはり裏返し操作が出来るとは思えない。
そもそも認識によって結果を変えようとするのは、明確に間違っているのでアプローチを変えてみる。
鏡あわせの宇宙を作ってみる
そんなことが可能か不可能かはさておき、パイプをのぞき込むように観測したときに鏡併せの空間が観測できるとする。
画像で表すとこんな感じ
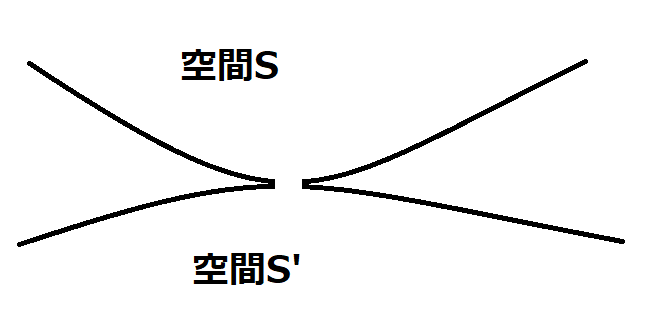
これで裏返し操作を試みる、こうすると空間SとS’の間に、交点が生じる。
上手く言語化できないが、この交点を空間Sから観測しつつ、穴を無限大に拡大する。
この時、空間Sの観測者は、必ず交点が存在する穴よりも大きいので「<>」←みたいな感じになるはずだ。
ここまで考えて気づいた、これをやったとしても「証明が出来ない」
穴の存在が座標系に依存するにも関わらず、証明を試みると別の座標系を求める必要がある。
これでは意味がない、やはり無理なのではないか
やはり無理か?
ここまで考えて私の頭には、ワームホールの理論が頭に浮かんだ。
だが、これは穴といえるのだろうか、これでは離れた空間が連続しているのみで、穴ではあるのだが落とし穴と一緒で観測地点によって穴が消失してしまう。
ググってみても有名なドーナツで例えた哲学的な思考実験が出てくる。
そもそも有形の概念を操作する数学的手法で、有形によって形成される現象である穴(無形的なもの)が有形に影響を与える操作はできないのではないか。
2日間考える
数学屋であれば、何か月も考えるのであろうが如何せん時間が足りないので要勉強という教訓を得て、今回の試みは終了としたのが現実だ。
おまけ
毎年フライトシムで初日の出フライトを行うのだが….. MSFSのアップデートをさぼった結果108GBのアップデートを大晦日に喰らって、無事フライト失敗である。
これまた煩悩たる108なのがなんとも言えない。
BIGイベントの計画や準備ははやめにやろう!
おわり














